Local Lucene Geographical Search
by Patrick O'Leary (pjaol at pjaol.com)
There are 3 components to how local lucene performs a geographical search.
- Create a bounding area.
- Query that areas document set for a text match.
- Reduce the document set to a precise distance from a center point.
Geographical text searching can take multiple formats, inclusion or reductionism.
Inclusion is applying text searching over a document set and verifying that the document fits within a predefined area.
e.g.
- Text match and is inside area.
Reductionism requires generating a set of documents bounded by an area, intersect that with a text search, and reduce the set of documents even further with a finer shape,
e.g.
- Inside large area
- Within a document set of text matches.
- Is inside a finer area.
Inclusion works well where your text search returns a close to discrete set of documents less than the total number of documents in the area your searching.
Reductionism works well where your text search may not be as discrete, and filtering out unnecessary documents by a simple bounding area reduces the amount of calculations you need to perform to determine if each individual document exists inside your area.
For instance, if you were generating demographics for the census bureau, and your document set was census data for all of the US.
With an ask of generate a report of the number of 20 year olds within 10 miles of point Manhattan NY.
In inclusion we start with, Ôgive me all 20 year olds in the entire USÕ, lets say 20 million results, now find all who live inside a 10 mile radius of point Manhattan NY.
That is 20 million calculations for an area, where the entire state population is only 8.2 million, thus your wasting more than 11.8 million intensive area calculations.
With reductionism we first define an area that will contain our results, we apply this to the document set, and intersect it with the results of our text search.
Now we have all results that fit in a larger area that meet our text search, next we apply our finer area calculation.
Applying this model to our example we start with defining a bounding area containing our search radius, and apply this to our document set, we go from a total document set of 301 million to say 6 million (Set A).
We now intersect this with all of the 20 year olds in the US (Set B),
Some basic 3rd grade math, A ‚ B, giving Set C (say 0.7 million) this is a very lightweight operation.
Set C is now reduced to highly valued results, which can again be reduced to the correct set of results using a more intensive area calculation.
Creating the bounding area.
There are multiple ways to create a bounding area, the 2 basic methods supported by local lucene are bounding box, and Cartesian area.
Boundary Box
A boundary box is defined as a box, which exists between an
upper left corner (lat 1 long 1) and a bottom right corner (lat2, long2), this
was the standard for local lucene R1.0. 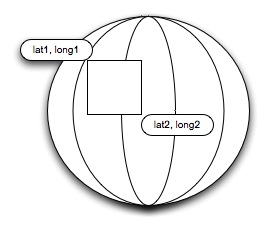
This required two passes through your data set, first pass find all latitudes between lat1 and lat2. The second pass is find all longitudes between long1 and long2 and merge the results. While this is a simple greater than or equals calculation, the number of unique latitudes and longitudes made this an extensive time consuming calculation. Which limits the size of your data set or compensates the length of time taken for getting results.
Cartesian Grid
A Cartesian grid goes a long way to try and resolve this. The first thing we do is project the world on a flat surface, using a Sinusoidal projection. Similar to a map layout.
 Courtesy
of Wikipedia, under commons license.
Courtesy
of Wikipedia, under commons license.
We create over lays to this projection of grids, called
Cartesian Tiers; each tier has an ever-increasing number of grid boxes on it.
Each tier has 2tier id number of grid boxes, dividing up the
projection.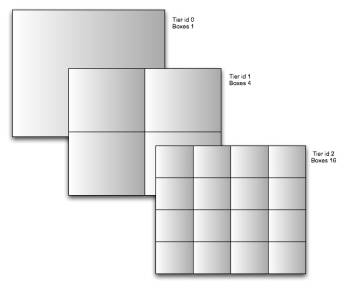 Tier 1 is a 2x2 grid, tier 2 4x4, tier 3 is 8x8 grid. We now have the ability
to place all of our data within these grids.
Tier 1 is a 2x2 grid, tier 2 4x4, tier 3 is 8x8 grid. We now have the ability
to place all of our data within these grids.
At tier level 15 we have a 32,768 x 32,768 grid, which translates to less than 1 mile square grid boxes.
So for instance, if you wanted to plot the location of everybody in the world, all 6 billion people, within a 1 mile square the most amount of grid boxes you will use, is over 1.07 billion. If you take into account that people will mainly exist on dry land, your only going to use 1/3rd of the boxes, so 6 billion unique locations can be represented by only 0.35 billion boxes throughout the globe.
Obviously there are vast regions of the earth unpopulated, and areas, which have high densities, that change the parameters of this projection.
Take for instance all businesses in the state of NY, currently that measures about 1.4 million businesses, in a traditional boundary box model, a search index would have to iterate through all 1.4 million latitudes, and longitudes for a radius search or 25 miles.
With a Cartesian search, the 25 miles is plotted as a series of grid boxes, and only those exact boxes are retrieved from the index. This plot might only consist of 9 boxes, thus reducing iterations from 2.8 million (number of lats + number of longitudes) cpu cycles, to 9 cpu cycles.
This vastly reduces the amount of time spent locating high value documents, so in a search of NY a 25 mile radial search can now find high value documents by looking for
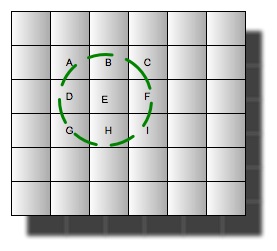 grids
specifically labeled as
grids
specifically labeled as
AÐI.
Box Id's
Box id's are an important component of Cartesian Tiers, standard Cartesian notation is broken into dimensions, Usually 2 dimensions, (X, Y)
Within Local Lucene, we specify these dimensions as a single double number X.Y, this also reduces the amount doc iteration needed within a document set, as you no longer need to iterate through 2 fields. The way this is achieved is by offsetting the Y coordinate by the upper magnitude that it can reach within a tier.
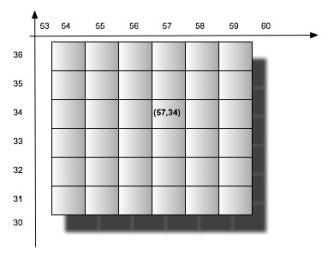 That
is, say you have a grid of 256 x 256 boxes, and a particular box located at
coordinates (57, 34), can now be represented by a single number. 57.034.
That
is, say you have a grid of 256 x 256 boxes, and a particular box located at
coordinates (57, 34), can now be represented by a single number. 57.034.
As you can see the Y coordinate is offset by 1,000, which is the upper magnitude (factor of 10) of maximum number of boxes that can exist at that tier id.
So for a 256x256 grid the upper magnitude would be 1,000, which is the highest power of 10^10 above the number of boxes in the Y axis.
So a 3,000x3,000 grid would have an upper magnitude of 10,000, a box with the coordinates (57,34) would now be represented as 57.0034 dividing the Y coordinate (34) by 10,000 and adding it to the X coordinate.